Introduction to Quantum Computing
Quantum Computing represents a paradigm shift from classical computing. Unlike classical computers, which use bits to process information, quantum computers use quantum bits or qubits. A bit in a classical computer can be either a 0 or a 1, representing a binary system. However, a qubit can represent 0, 1, or both 0 and 1 simultaneously, thanks to a phenomenon called superposition (Jones & Matthias, 2018).
2. Quantum Phenomena and Qubits
The primary principles that allow quantum computers to function are superposition, entanglement, and quantum interference.
Superposition: Unleashing Quantum Parallelism
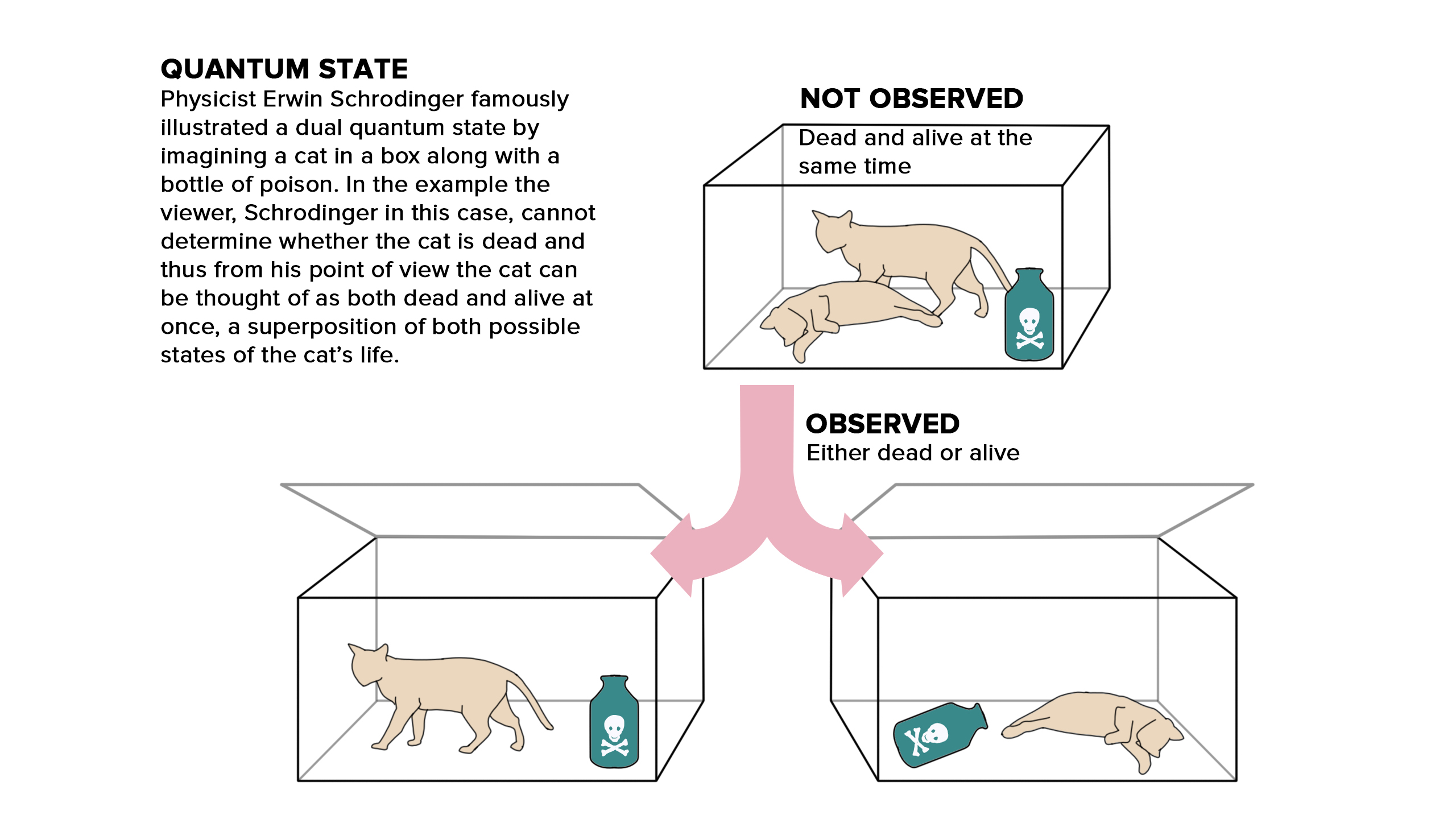
Superposition, a cornerstone concept in quantum mechanics, radically diverges from our intuitive understanding of the binary world we inhabit. In classical computing, a bit, the smallest unit of information, can exist in one of two states: 0 or 1. Quantum computing, however, introduces the quantum bit or qubit. Unlike its classical counterpart, a qubit can exist not only in a state representing 0 or in a state representing 1, but also in a superposition of both these states simultaneously.
To truly grasp the implications of superposition, let's consider a thought experiment. Imagine a vast library with millions of books. In a classical computer, searching for a particular book is analogous to checking each book one-by-one. But with a quantum computer, thanks to superposition, it's as if you can check numerous books at the same time. Each qubit added doubles the parallel processing capability: 2 qubits can be in 4 states simultaneously (00, 01, 10, or 11); 3 qubits in 8 states, and so forth. This exponential growth means quantum machines, theoretically, could process vast amounts of data in parallel.
However, superposition is not merely about being in multiple states at once. The true marvel lies in the ability to represent and process a vast amount of information with a relatively small number of qubits. Each qubit can hold a superposition of states, and when multiple qubits are entangled — another quantum phenomenon — they can represent an even more enormous array of binary combinations, all at once.
The catch, and the challenge, is reading the outcome. Once observed, a qubit in superposition collapses to one of its basis states, either 0 or 1, following probabilistic rules determined by its quantum state before measurement. This means that even though a quantum computer can process a multitude of possibilities simultaneously, we still need innovative algorithms to ensure that the solution we seek is the one most likely to be observed.
Superposition offers a promise of unprecedented computational power, but with it comes the challenge of harnessing and directing that power to solve real-world problems. The delicate nature of superpositions, susceptible to environmental interference, makes error correction crucial in quantum computing. But, with advances in quantum error correction and fault-tolerant algorithms, we are progressively moving closer to harnessing the true potential of superposition for a new era of computing.
Entanglement: The Mysterious Quantum Link

Entanglement, a term that even baffled the likes of Albert Einstein, who famously dubbed it "spooky action at a distance," is a uniquely quantum phenomenon and serves as another fundamental pillar of quantum mechanics. At its core, entanglement describes the phenomenon where pairs or groups of particles become interlinked in such a way that the quantum state of one particle cannot be described independently of the others, regardless of the distance separating them.
To visualize this, consider a pair of entangled dice. In the quantum realm, if you roll these dice without looking at the results, each die can exist in a state representing all its possible outcomes due to superposition. However, the moment you observe one die and see, for example, a 3, its entangled counterpart will instantaneously "decide" its value, based on the outcome of the first, even if they're separated by vast cosmic distances. This immediate determination of states violates our classical intuition and even appears to challenge the limitations set by the speed of light.
But why is entanglement so pivotal for quantum computing? In the realm of quantum algorithms and computation, entangled qubits allow for intricate choreographies of coordinated actions. It's akin to having synchronized dancers, where the move of one instantly influences the other, irrespective of the distance between them. This interconnectivity aids in solving complex problems where variables are interdependent, allowing quantum computers to potentially outperform classical machines that view each variable in isolation.
Entanglement's practical applications don't just stop at computing. It's a foundational concept for emerging technologies like quantum teleportation and quantum cryptography. In quantum cryptography, the principle of entanglement is exploited to detect eavesdroppers, as any attempt to intercept a quantum communication disrupts the delicate state of entangled particles, alerting the communicators of potential security breaches.
Despite its foundational role in quantum mechanics, entanglement remains one of the least understood phenomena. It defies classical intuition, pushing the boundaries of our understanding of nature. Yet, it's this very enigma that promises a revolution in computation and communication, redefining the boundaries of what's achievable.
Quantum Interference: The Delicate Dance of Waves

Quantum interference lies at the heart of many quantum phenomena and is pivotal to the operations of quantum computers. Drawing its roots from wave-particle duality, quantum interference is about the constructive and destructive interaction of probability amplitudes. This may sound perplexing, so let's unpack it.
To start, consider the classical analogy of water waves. If two waves meet and are in phase (i.e., their peaks and troughs align), they will amplify each other, resulting in a wave of increased amplitude. Conversely, if they are out of phase (a peak meets a trough), they will diminish or even cancel each other out. This is classical interference. Now, quantum particles, like electrons or photons, exhibit similar interference patterns, not because they are spreading out like waves but because their probability amplitudes interfere.
Now, let's transition this idea into the quantum world of qubits. A qubit can be in a superposition of both its |0⟩ and |1⟩ states. When a quantum system evolves, these states, described by their respective wave functions or probability amplitudes, can combine in ways where they reinforce or cancel out each other. The outcome of a quantum computation is influenced by the careful choreography of these amplitudes to ensure that the desired computational paths (those leading to correct solutions) constructively interfere, while paths leading to wrong answers destructively interfere.
The magic of quantum interference is fully realized in algorithms like Grover's and Shor's. For instance, in Grover's algorithm, a database search task, interference is employed to amplify the probability amplitude of the correct answer, making it more likely to be observed, while suppressing the wrong answers.
Harnessing quantum interference in practical scenarios isn't straightforward. The delicacy of quantum states means they're highly susceptible to external influences. Any disturbance, be it thermal, electromagnetic, or even cosmic rays, can disrupt the desired interference patterns, leading to errors in computations. This has driven researchers to explore methods like quantum error correction and to develop quantum-resistant cryptographic algorithms.
In essence, quantum interference is both a blessing and a challenge. It's a foundational phenomenon enabling the speed-ups of quantum computation, but at the same time, its delicate nature requires us to tread carefully, ensuring that as we manipulate these quantum states, we maintain their integrity to achieve the desired outcomes.
To be continued with part 2!